Discussion
Last updated on 2024-03-05 | Edit this page
Rules of Debugging
- Fail early, fail often.
- Always initialize from data.
- Know what it’s supposed to do.
- Make it fail every time.
- Make it fail fast.
- Change one thing at a time, for a reason.
- Keep track of what we’ve done.
- Be humble.
- Test the simple things first.
And remember, a week of hard work can sometimes save you an hour of thought.
The Call Stack
Let’s take a closer look at what happens when we call
fahr_to_celsius(32.0). To make things clearer, we’ll start
by putting the initial value 32.0 in a variable and store the final
result in one as well:
The diagram below shows what memory looks like after the first line has been executed:
When we call fahr_to_celsius, Python doesn’t
create the variable temp right away. Instead, it creates
something called a stack frame
to keep track of the variables defined by fahr_to_kelvin.
Initially, this stack frame only holds the value of
temp:
When we call fahr_to_kelvin inside
fahr_to_celsius, Python creates another stack frame to hold
fahr_to_kelvin’s variables:
It does this because there are now two variables in play called
temp: the parameter to fahr_to_celsius, and
the parameter to fahr_to_kelvin. Having two variables with
the same name in the same part of the program would be ambiguous, so
Python (and every other modern programming language) creates a new stack
frame for each function call to keep that function’s variables separate
from those defined by other functions.
When the call to fahr_to_kelvin returns a value, Python
throws away fahr_to_kelvin’s stack frame and creates a new
variable in the stack frame for fahr_to_celsius to hold the
temperature in Kelvin:
It then calls kelvin_to_celsius, which means it creates
a stack frame to hold that function’s variables:
Once again, Python throws away that stack frame when
kelvin_to_celsius is done and creates the variable
result in the stack frame for
fahr_to_celsius:
Finally, when fahr_to_celsius is done, Python throws
away its stack frame and puts its result in a new variable
called final that lives in the stack frame we started
with:
This final stack frame is always there; it holds the variables we
defined outside the functions in our code. What it doesn’t hold
is the variables that were in the various stack frames. If we try to get
the value of temp after our functions have finished
running, Python tells us that there’s no such thing:
ERROR
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-12-ffd9b4dbd5f1> in <module>()
----> 1 print('final value of temp after all function calls:', temp)
NameError: name 'temp' is not definedOUTPUT
final value of temp after all function calls:Why go to all this trouble? Well, here’s a function called
span that calculates the difference between the minimum and
maximum values in an array:
PYTHON
import numpy
def span(a):
diff = numpy.amax(a) - numpy.amin(a)
return diff
data = numpy.loadtxt(fname='inflammation-01.csv', delimiter=',')
print('span of data:', span(data))OUTPUT
span of data: 20.0Notice that span assigns a value to a variable called
diff. We might very well use a variable with the same name
to hold data:
PYTHON
diff = numpy.loadtxt(fname='inflammation-01.csv', delimiter=',')
print('span of data:', span(diff))OUTPUT
span of data: 20.0We don’t expect diff to have the value 20.0 after this
function call, so the name diff cannot refer to the same
thing inside span as it does in the main body of our
program. And yes, we could probably choose a different name than
diff in our main program in this case, but we don’t want to
have to read every line of NumPy to see what variable names its
functions use before calling any of those functions, just in case they
change the values of our variables.
The big idea here is encapsulation, and it’s the key to writing correct, comprehensible programs. A function’s job is to turn several operations into one so that we can think about a single function call instead of a dozen or a hundred statements each time we want to do something. That only works if functions don’t interfere with each other; if they do, we have to pay attention to the details once again, which quickly overloads our short-term memory.
Image Grids
Let’s start by creating some simple heat maps of our own using a
library called ipythonblocks. The first step is to create
our own “image”:
Unlike the import statements we have seen earlier, this
one doesn’t load the entire ipythonblocks library. Instead,
it just loads ImageGrid from that library, since that’s the
only thing we need (for now).
Once we have ImageGrid loaded, we can use it to create a
very simple grid of colored cells:

Just like a NumPy array, an ImageGrid has some
properties that hold information about it:
PYTHON
print('grid width:', grid.width)
print('grid height:', grid.height)
print('grid lines on:', grid.lines_on)OUTPUT
grid width: 5
grid height: 3
grid lines on: TrueThe obvious thing to do with a grid like this is color in its cells, but in order to do that, we need to know how computers represent color. The most common schemes are RGB, which is short for “red, green, blue”. RGB is an additive color model: every shade is some combination of red, green, and blue intensities. We can think of these three values as being the axes in a cube:
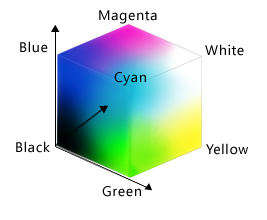
An RGB color is an example of a multi-part value: like a Cartesian coordinate, it is one thing with several parts. We can represent such a value in Python using a tuple, which we write using parentheses instead of the square brackets used for a list:
PYTHON
position = (12.3, 45.6)
print('position is:', position)
color = (10, 20, 30)
print('color is:', color)OUTPUT
position is: (12.3, 45.6)
color is: (10, 20, 30)We can select elements from tuples using indexing, just as we do with lists and arrays:
OUTPUT
first element of color is: 10Unlike lists and arrays, though, tuples cannot be changed after they are created — in technical terms, they are immutable:
ERROR
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-11-9c3dd30a4e52> in <module>()
----> 1 color[0] = 40
2 print('first element of color after change:', color[0])
TypeError: 'tuple' object does not support item assignmentIf a tuple represents an RGB color, its red, green, and blue components can take on values between 0 and 255. The upper bound may seem odd, but it’s the largest number that can be represented in an 8-bit byte (i.e., 28-1). This makes it easy for computers to manipulate colors, while providing fine enough gradations to fool most human eyes, most of the time.
Let’s see what a few RGB colors actually look like:
PYTHON
row = ImageGrid(8, 1)
row[0, 0] = (0, 0, 0) # no color => black
row[1, 0] = (255, 255, 255) # all colors => white
row[2, 0] = (255, 0, 0) # all red
row[3, 0] = (0, 255, 0) # all green
row[4, 0] = (0, 0, 255) # all blue
row[5, 0] = (255, 255, 0) # red and green
row[6, 0] = (255, 0, 255) # red and blue
row[7, 0] = (0, 255, 255) # green and blue
row.show()
Simple color values like (0,255,0) are easy enough to
decipher with a bit of practice, but what color is
(214,90,127)? To help us, ipythonblocks
provides a function called show_color:

It also provides a table of standard colors:
PYTHON
from ipythonblocks import colors
c = ImageGrid(3, 2)
c[0, 0] = colors['Fuchsia']
c[0, 1] = colors['Salmon']
c[1, 0] = colors['Orchid']
c[1, 1] = colors['Lavender']
c[2, 0] = colors['LimeGreen']
c[2, 1] = colors['HotPink']
c.show()
